"לימוד המכונה מוצא את היער בין העצים גם בפיזיקה תיאורטית"

ד"ר זוהר רינגל, מרצה בכיר במכון רקח לפיזיקה באוניברסיטה העברית גילה כי מכונות לומדות יכולות לעזור להבין מהם המשתנים החשובים מתוך הרעש הסטטיסטי שמפריע להבין את המגמה הכללית, וגם להפך – להשתמש בתובנות אלה כדי לשפר את יכולות לימוד המכו.

"מטרת המדע היא לפשט את תיאור הבעיה (רדוקציה), כדי להסביר בעיות קשות באמצעות משוואות בעלות מספר קטן מאוד של משתנים", מסביר ד"ר רינגל בראיון לאתר הידען. לדוגמה, "כדי לתאר באופן מושלם זרימה של מים בנהר עלינו באופן עקרוני לעקוב אחרי כל מולקולה. עם זאת כדי להבין איך המים מתנהגים בסקאלות אורך מאקרוסקופיות, מספיק לעקוב אחרי פונקציה בודדת – פונקציית מהירות הנוזל במרחב".

"דוגמה אחרת הנה מתחום הכלכלה", אמר. "כשנגיד בנק מרכזי מנסה לעמוד על מצבה של כלכלה, הוא לא צריך לדעת מה מתרחש במיליוני חשבונות בנק, אלא מסתכל על מדדים כלליים כגון התל"ג ומדד ג'יני לאי-שיוויון כדי לאבחן האם הכלכלה פועלת במיטבה. באופן דומה גם בניסיונותיו להשפיע על הכלכלה הוא לא חושב על כל אדם בנפרד אלא על פרמטרי שוק כגון שער הריבית. באופן זה הוא מבצע רדוקציה מבעיה מסובכת מרובת משתנים לבעיה פשוטה יותר עם מעט משתנים ופרמטרים".

רינגל הסביר כי "כדי להשיג את אותה הרדוקציה באופן שיטתי, פיזיקאים משתמשים בטכניקה הנקראת RG (ר"ת Renormalization group). הטכניקה הזו מאפשרת לנו למצוא מהן המשתנים החשובים לתיאור הדינמיקה של הבעיה תוך ניסיון לשמור שיהיו כמה שפחות כאלה".

טכנולוגיית ה-Renormalization group. צילום באדיבות: ד"ר זוהר רינגל

"ניקח דוגמה תיאורטית שפתרו בשנות ה-80 המוקדמות. נניח שאני מתאר לך גז דמיוני שניתן לתאר את חלקיקיו כמוטות הנעים על מבנה דו-מימדי העשוי ממשושים. החלקיקים זזים ומשנים את מיקומם. צריך למצוא דרך יעילה לתיאור המערכת הזו – למשל מה קורה אם אני דוחף את אחד המוטות במקום מסוים, מה ארגיש במקום אחר"?

"ישנו תכסיס גרפי פשוט העוזר לחשוף את התיאור הנכון", אמר. "הבה נקיף כל מוט במעוין, כאשר צבע המעוין תלוי בזווית המוט. אופן ייצוג זה של הבעיה מיד גורם לציור לבלוט החוצה ולהפוך לתלת-מימדי. עם זאת, עדיין המשטח שנוצר הוא מאוד מחוספס, בדיוק כפי שמים יראו לא אחידים ברזולוציה של המולקולות. המהלך הנוסף לקבלת תיאור פשוט של הבעיה הוא, כמו במים, לרדת ברזולוציה ולראות שכל החלקיקים הללו יוצרים משטח אלסטי שיש בו עליות ומורדות. כעת תיאור הבעיה ניתן על ידי פונקציה בודדת – גובה המשטח בכל נקודה".

במחקר שלנו, אמר רינגל, "שאלנו האם בשיטות של לימוד מכונה ניתן למצוא תיאורים יעילים מסוג זה, באופן אוטומטי בהקשר של בעיות בפיזיקה. ביקשנו מתוכנה לקחת בעיות ולגלות בעצמה לנו שהנתון החשוב ביותר הוא הגובה. תכננו אלגוריתם לביצוע המשימה שמשתמש בשיטות מתורת האינפורמציה ולימוד מכונה ונסינו אותו על שלוש בעיות שונות לגמרי בפיזיקה – ובכל המקרים, האלגוריתם גילה מחדש את מה שפיזיקאים תיאורטיקנים גילו. ובכל המקרים היו אלו תגליות לא טריוויאליות, ויש לציין שהמחשב עשה זאת בחלקיק מהזמן שלקח למדענים לגלות את התכונה המקורית".

מה השימוש לאלגוריתם כזה?
"יש כמה היבטים לשימוש כזה – ראשית לטובת הפיזיקה. יש המון בעיות בהן אנחנו לא יודעים מהם המשתנים החשובים או כמה מהם צריך כדי לקבל ייצוג מהימן של הבעיה. זאת ארץ לא נודעת, וייתכן ושיטות של לימוד מכונה יעזרו לנו לפצח כמה בעיות קשות שכאלה".

"בנוסף, ניתן למפות בעיות אופטימזציה רבות כגון הסוכן הנוסע (מציאת המסלול הקצר ביותר בין מספר ערים על מפה) לבעיות בפיזיקה הדומות לבעיית המוטות שהזכרנו קודם".

"מציאת המשתנים הרלוונטים בבעיות שכאלו משמעה שיפור היכולת שלנו לפתור בעיות אופטימזציה גדולות באופן יעיל. לדוגמה, ייתכן ובעיית סוכן נוסע שצריך לעבור בין מיליון ערים, מתחלקת באופן טבעי ל-1,000 קבוצות ערים שונות. בחלוקה לקבוצות ערים, מיקומה הממוצע של כל קבוצת ערים שכזו יהיה משתנה חשוב בבעיה. אסטרטגיה אפשרית לפתור את בעיית האופימיצזיה תהיה אם כן קודם כל למצוא את המסע הקצר ביותר בין קבוצות הערים הללו ורק לאחר מכן לפתור את הבעיה של איך לנוע ביעילות בתוך כל קבוצה בנפרד. ההשלכה של כך על זמן החישוב הדרוש לפתור את הבעיה יכולה להיות אדירה".

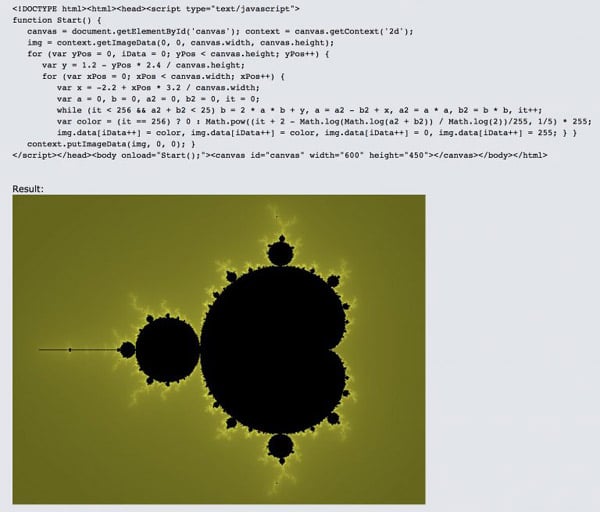
הפרקטל של מנדלברוט. צילום באדיבות: ד"ר זוהר רינגל

"כיוון שמעניין לא פחות הוא דווקא הכיוון ההפוך. אם יש קשר עמוק בין לימוד מכונה לזיהוי משתנים רלוונטיים בבעיות בפיזיקה, אולי נוכל להבין מה קורה בתוך מכונות לומדות תוך שימוש בטכניקות מפיזיקה תיאורטית כגון RG. כך יהיה ניתן להשים על בסיס תיאורטי איתן את עקרונות התכנון של מכונות לומדות מסובכות כגון רשתות ניורונים עמוקות".

משהו לא ברור, איך איננו יודעים כיצד פועל אלגוריתם לימוד מכונה אם בני אדם יצרו אותו?
"ברור שהמתכנת מבין כל פרט 'אטומי' בתוכנה שלו כגון IF ו-ELSE או לולאות FOR, אבל כאשר הקוד מורכב – כלל לא פשוט להבין מה יהיה הפלט הסופי. דוגמה – קוד פשוט מאוד של 14 שורות ב-JavaScript מאפשר לצייר את הפרקטל של מנדלברוט בעוד שהצורה מאוד יפה, מורכבת, ולא צפויה".